Tomoki Kawahira
/ Graduate School of Economics / Hitotsubashi University
Tomoki Kawahira
/ Graduate School of Economics / Hitotsubashi University
複素関数論の基礎から初めて，
後半はリーマン面について解説しました．
第12回(
2015年3月号)
群で作るリーマン面
● 1次分数変換の部分群を複素平面に作用させて，
トーラス，格子トーラス，
種数 2 の閉リーマン面を具体的に構成します．
第11回(
2015年2月号)
リーマン球面と1次分数変換
● 「複素平面＋無限遠点」としてリーマン球面を定式化し，
有理型関数の概念を別の視点から眺めます．
● {z -> z + n} の形の平行移動による
軌道空間として，リーマン面（円柱）を構成します．
第10回(
2015年1月号)
1次元複素多様体としてのリーマン面
● ワイル流に，「多様体」の概念を用いてリーマン面を構成し，
その上の正則関数とは何かを丁寧に（くどめに？）解説します．
ちなみに，「位相空間」や「ハウスドルフ空間」といった言葉は持ち出しません．
（たぶんワイルの時代に，そのような言葉はなかったはずです．）
第9回(
2014年12月号)
解析接続とリーマン面（2）
● リーマン流の「切り貼り」によるリーマン面の構成方法を解説します．
「多価関数を一価関数のように扱う」ために，
定義域のほうを拡張する，
というのがリーマンのアイディアです．
1次元版の「リーマン線」から始めて，くどめに説明しました．
● 代数方程式の解として得られる多価関数（代数関数）
のリーマン面の例として，種数1のリーマン面が出てくる例を扱いました．
じつは種数1といっても，いわゆるトーラスではないのです．
（なぜなら，無限遠点やリーマン球面をまだやってないから．．）
第8回(
2014年11月号)
解析接続とリーマン面（1）
● 今回から後半戦で，リーマン面の話に入ります．
ゼータ関数をひとつの成功例として，解析接続について解説します．
とくに，自然境界の問題と多価性の問題に焦点をあてます．
● 多価性をもつ関数のもっとも簡単な例として，
平方根についてくわしく解説しました．
次回はこの例を念頭に，平方根のリーマン面を構成します．
第8回(
2014年11月号)
解析接続とリーマン面（1）
● 今回から後半戦で，リーマン面の話に入ります．
ゼータ関数をひとつの成功例として，解析接続について解説します．
とくに，自然境界の問題と多価性の問題に焦点をあてます．
第7回(
2014年10月号)
留数定理と実積分への応用
● ローラン展開により（孤立）特異点の分類をし，留数を定義，
さらに留数定理を定式化しました．
● 三角関数を含む積分，有理関数の広義積分への典型的な応用例を紹介しました．
● 「簡単に求まらない広義積分」の代表ともいえる，ガウス積分を複素積分で計算しました．
本稿では「おそらくポリア（ポーヤ）の1949年の論文が最初」のようなことを書きましたが，
初版が大正時代という古典的名著，竹内端三の「函数論（上・下）」（裳華房）にもポリアの方法に近い形でガウス積分を求める演習問題がありました．
まさかと思いよく調べたところ，初版にこの問題は書かれておらず，
昭和30年前後の改訂・増刷あたりで加えられたようです．
したがって「ポリアが最初」という仮説はいまだ否定されておりません．
まあ天国のポリアさんご自身も，気にはしないでしょうが．
第6回(
2014年9月号)
一致の定理・最大値原理，ローラン展開
● まずはテイラー展開の収束円の境界には「特異点」があることを確認．
次回紹介するように，特異点は「面白い」積分値（留数）を
生み出す源泉です．
● 一致の定理と最大値原理を解説．
ここは正則関数の特殊性が際立つ部分だと思います．
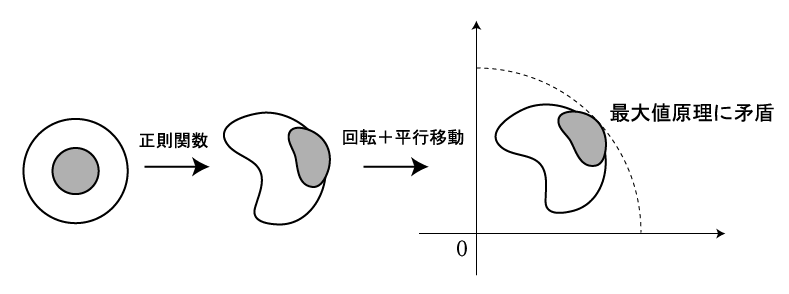
● 76ページ図3にある「正則関数で，黄身は飛び出ない」
ことの理由を説明しましょう．
正則関数 f で図3の左から図3の右のように写像されたと
仮定すると，さらに適当な回転＋平行移動 g（これは1次関数で表現される）
をほどこすと黄身の部分が「最大絶対値」を与えるようにできます．
仮定より g(f(z)) は正則ですがこれは「最大値原理」に反するので矛盾，というわけです．
複素力学系理論では，このような正則関数の「位相的性質」が重要な役割を果たします．
たとえば多項式のジュリア集合やマンデルブロー集合の形にも，
「黄身が飛び出ない」性質が反映されているのです．
● 次回の留数定理に向けて，ローラン展開を証明しました．
脚注ではローランがどんな人だったか簡単に紹介してみました．
Wikipediaによると，
ワイエルシュトラスはローランよりも先にローラン展開を知っていたようです．
第5回(
2014年8月号)
積分公式からテイラー展開へ
● 高階微分の積分公式（グルサの公式）を帰納法で直接証明しました，
n = 1 の場合だけやって「あとは帰納法で」とごまかす教科書が多いのですが
（もしくは，べき級数の一般論を展開したあとでテイラー展開の存在を示し，
その係数から高階微分の積分公式を導く），
本稿では一般の n で通用する比較的簡単な計算方法を考えてみました．
（それでもまだ難しいかな．．）
● リュービルの定理，代数学の基本定理を証明しました．
今回代数学の基本定理の歴史をいろいろ調べてみましたが，
なかなか奥が深いです．
アルガンというアマチュア数学者が登場します．
● テイラー展開の証明．
つい罪悪感に負けてしまって，
一様収束などの数学的に細かい部分について書いてしまいました．
積分と無限和の交換を正当化するためですが，
関数論の面白さより面倒くささを強調してしまったかもしれません．
第4回(
2014年7月号)
コーシーの積分定理・積分公式
● 「積分定理」をグルサ流に，グリーンの定理を使わずに証明します．
● 「積分定理」の成立には，原始関数の存在が本質的です．
さらに閉曲線での積分値が 0 になるという現象を「ハイキングの原理」で説明しました．ちなみに「ハイキングの原理」というのは私が勝手につけた名前です．
数学的には線積分や勾配ベクトルを理解してないと少し難しいかも．
● 続いて「積分定理」の応用として単連結領域上の正則関数の積分が積分路の端点だけで決まることと，「積分公式」を証明しました．
第3回(
2014年6月号)
正則関数の積分定理
● 『複素関数論とは，「正則関数」の理論である．』と冒頭からキメてみました．
● 正則関数を定義．正則なら連続の確認．初等関数の微分公式を確認．
● 他に類を見ない罪悪感あふれる図（※イメージです）
で複素線積分とコーシーの積分定理を理解しましょう．
図というのはあくまで「記憶の助け」であって，
「794（鳴くよ）ウグイス・ホーホケキョ(?)」
と同じレベルなんだと思います．
第2回(
2014年5月号)
複素関数の微分
● 訂正： 69ページ11行目，limの下の x は z の間違いです．
● 実1変数関数のグラフを顕微鏡で拡大するところからスタート．
顕微鏡の中には比例関数が見えている．
● 複素関数の比例関数とは何か？それは平面を拡大・回転する写像である．
● 複素関数を顕微鏡で観察する．
ある点で「複素微分可能」であるとは，
顕微鏡の中に複素関数の比例関数が見えているときをいう．
● 「複素微分可能性」を実2変数写像の言葉で言い換えると，
「ヤコビ行列が拡大・回転を表す行列になっていること」
となる．その行列の形から，いわゆるコーシー・リーマンの方程式を導出．
このあたりの計算はゴチャゴチャしていて，
雑誌連載としては罪悪感を覚えてしまいますが，
われわれ「1次変換（を高校で習った）世代」としては
ビジュアル的にもこれ以上分かりやすい方法はないと思います．
「全微分」なんかもできれば使わずに済ませたかったのですが，
限界がありますね．
● 正則関数の定義までやりたかったのですが，
ページが足りずコーシー・リーマンと指数関数の微分係数の計算までにしました．
第1回(
2014年4月号)
オイラーの公式と指数関数
● 「数学でもっともすごい」オイラーの公式を視覚的に理解することを目標にしました．
● 複素数の基礎事項を軽くおさらいしたあと，
複素数列と複素級数を定義．三角不等式を確認．
複素級数は「折れ線」で表現できるところがポイント．
● 複素の指数関数を級数で定義し，
その収束性を絶対収束性を示すことで証明．
オイラーの公式を「折れ線」で表現した．
● 指数関数の周期性，三角関数の定義など．
● 初回ということもあり，試行錯誤からのスタート．
「である調」にするか，「ですます調」にするか，
締め切り直前までくよくよと悩みました．
「よこがお」欄ではプラトンの対話編『メノン』について書きましたが，
大栗氏による巻頭言にもこれが登場していてびっくり，嬉しかったです．
新しい概念を既知の概念から理解する，
という視点は認知科学的にもっと掘り下げられてもいいテーマだと思います．