Tomoki Kawahira
/ Graduate School of Economics / Hitotsubashi University
Tomoki Kawahira
/ Graduate School of Economics / Hitotsubashi University
1変数および多変数の関数について，微分積分学の基礎を学びます．
講義で配布したプリントをまとめたもの：
PDF
※ 予習用ビデオのURLは受講者に直接告知しております．
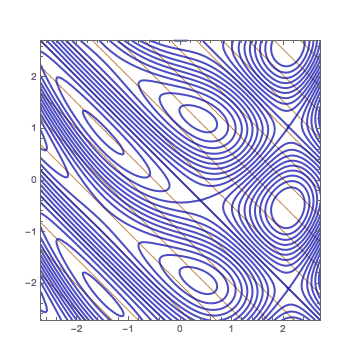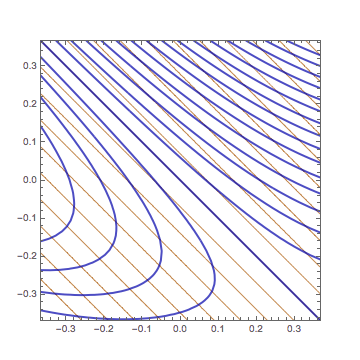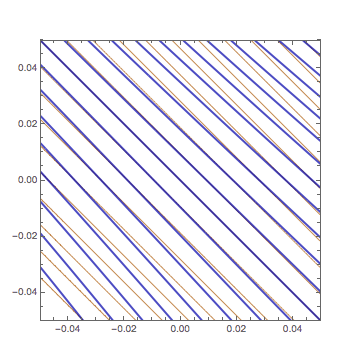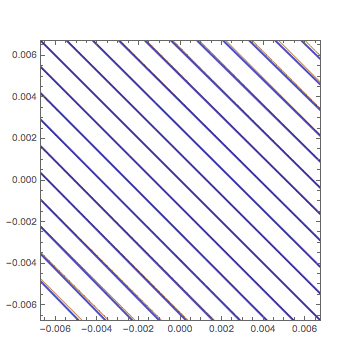
See more GIF animations
第1回(2020/5/4) 写像と関数，いろいろな関数
● 予習用ビデオ：
第1部（一変数の微分積分），「2. 数の集合」〜「7. 初等関数(2)」
● コメント：
区間の記号，連続関数について復習します．
また，おなじみの指数・対数・三角関数に加え，逆三角関数について学びます．
アンケートなど実施しました．Zoomへの接続状況：100名受講者がいて，
Windowsパソコン 7割，Mac 2割，スマホ が 5名，タブレット 5名というかんじでした．
タイピングに慣れていない学生さんも多いようです（「微分積分学って面白いですね。」と
タイプするのに20秒以上かかる人が約2割）．
第2回(2020/5/8) 初等関数の微分と積分，有理関数等の不定積分
● 予習用ビデオ：
第1部（一変数の微分積分），「8. 微分と1次近似(1)」〜「11. 不定積分」
● コメント：
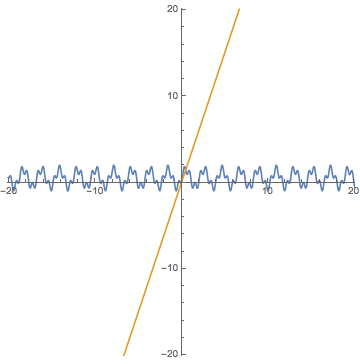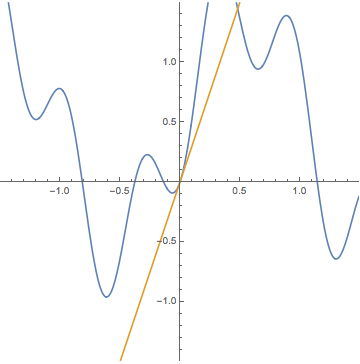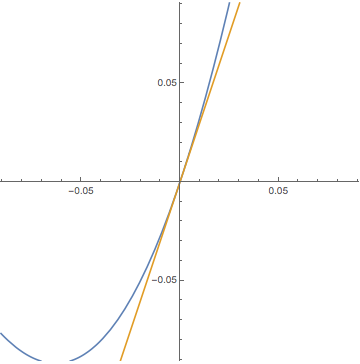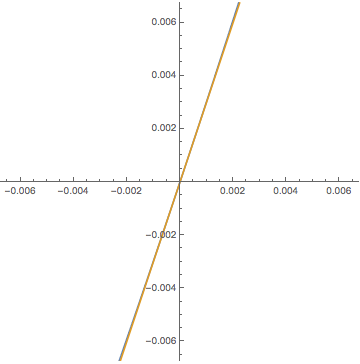
微分可能性の定義を
接線の方程式（関数の1次近似）が自然に現れる形にアップデートします．
また，不定積分（原始関数）について学びます．
投票の結果など：チャットのURLからリンクに飛べない人が6割以上．
コピペで対応している．ファイルの送信はうまくいかない様子．
4分の1の人たちが講義内課題もといて予習ばっちり，
4分の1の人たちが予習なしで講義に挑む，あとはその中間という感じです．
予習なしだと，これから辛くなりますよ．
第3回(2020/5/11) 定積分,広義積分
● 予習用ビデオ：
第1部（一変数の微分積分），
「12. 定積分(1)」〜「17. 広義積分(2)」．
余裕があれば「18. ガンマ関数(1)」，「19. ガンマ関数(2)」も観ておくとよい．
● コメント：
定積分の定義を確認したあと，
微分積分学の基本定理について学びます．
また，広義積分の定義と具体例を確認します．
加えて，優収束の方法についても解説しました．
受講者のうち86%のみなさんが毎週 10 コマ以上のZoom講義を受講しているようです．
第4回(2020/5/15) 多変数関数，極限，連続性
● 予習用ビデオ：
第2部（多変数の微分），
「4. 多変数の極限1」と「5. 多変数の極限2」．
記号は私（川平）の講義と違う部分がありますが，
概念の意味づけについてとても丁寧に解説されています．
余裕があれば「1. イントロ」〜「3. 数学的イントロ」も観ておくとよい．
● コメント：
2変数の1次関数の等高線の形について問題を考えてもらいました．
関数の極限・連続性については中途半端になってしまったので，
次回また補足します．
微分積分学第二の講義がオンライン・対面で選べるとしたら，
４割のひとがオンライン，６割の人が対面，とのことでした．
第5回(2020/5/18) 多変数関数の全微分
● 予習用ビデオ：
第2部（多変数の微分），
「6. 全微分vs偏微分1」，
「7. 全微分vs偏微分2」，
「9. 全微分可能性vs偏微分可能性」．
記号は私（川平）の講義と違う部分がありますが，
概念の意味づけについてとても丁寧に解説されています．
余裕があれば「8. 一般方向の偏微分」も観ておくとよい．
● コメント：
前回の復習と，やり残した連続性の定義からスタート．
そのあと，全微分について学びました．
非常に大事な部分なのでゆっくりやりました．
偏微分についてのノートや課題も準備していましたが，
終わらなかったので次回に回しました．
第6回(2020/5/22) 多変数関数の偏微分
● 予習用ビデオ：
第2部（多変数の微分），
「10. 高階の偏微分」
「11. 高次近似」は微分積分学第二の内容ですが，
余裕があれば観ておくとよいです．
● コメント：
軽く前回の復習をした後，
多変数関数の偏微分の定義と意義（全微分可能性が判定できる），
高階偏微分を学びました．
第7回(2020/5/25) 合成関数の導関数（連鎖公式）
● 予習用ビデオ（参考）：
第2部（多変数の微分）の 「12. 線形代数速成1」〜「19. 連鎖律の例」が対応しますが，
一般化された議論をしているので，少し難しめです．
ビデオはあくまで参考，ということにして，
予習は講義ノートの方をメインにしてください．
なお，第2部の14, 15, 20, 21 は微分積分学第二
あるいはそれ以上の内容となります．
● コメント：「1変数->2変数->1変数」型の合成関数の微分公式と，
変数変換を伴う「2変数->2変数->1変数」型の
合成関数の偏微分公式の解説と，関連する課題に取り組みました．
予習用ビデオか予習用講義ノート，
どちらか一つ選ぶならビデオという人がが14%，ノートという人が86%．
ビデオを作成した我々としては，微妙な結果がでました．
第8回(2020/5/29) 多変数関数の積分
● 予習用ビデオ：
第3部（多変数の積分），
「1. 積分の定義と例1」と「2. 積分の定義と例2」
● コメント：偏微分の合成関数について少し前回の続きをやったあと，
重積分の定義を学びました．「面積確定」，連続関数の積分可能性はゆっくりやる時間がなかったので次回に．
第9回(2020/6/1) 重積分と累次積分，積分順序の交換
● 予習用ビデオ：
第3部（多変数の積分），「3. 累次積分」
● コメント：前回の復習のあと，累次積分を導入します．
これにより，縦線集合・横線集合上の重積分が計算できるようになります．
第10回(2020/6/5) 重積分の変数変換 (1)
● 予習用ビデオ：
第3部（多変数の積分），
「4. 2変数の変数変換1」と「5. 2変数の変数変換2」．
● コメント：累次積分の計算の続きをしたあと，
変数変換のヤコビアンの意味と重積分の変数変換の公式とその意味について学びました．
計算方法についてはまた次回いろいろ学びます．
第11回(2020/6/8) 積分の変数変換 (2)
● 予習用ビデオ：
第3部（多変数の積分），
「6. 2変数の変数変換3」
● コメント：変数変換の復習をしたあと，ハイライトとも言える「ガウス積分」の計算をやりました．
また，球の体積の計算をやりました．
第12回(2020/6/12) 3変数の微分積分
● 予習用ビデオ：
第3部（多変数の積分），
「7. 3変数の変数変換1」〜「8. 3変数の変数変換2」．
「9. 3変数の変数変換3」〜「10. 3変数の変数変換4」．
● コメント：3変数の微分（全微分＋偏微分）について簡単に解説したあと，
３重積分の具体的な計算方法について学びます．ヤコビアンを定義したところで終わったので，残りは次回にまわしましょう．
第13回(2020/6/15) 曲面積
● 予習用ビデオ：
第3部（多変数の積分），
「11. 曲面積 1」〜「13. 曲面積 3」
● コメント：
前回の復習をしたあと，曲面の面積の定義と計算方法を学びました．
第14回(2020/6/19) 期末試験（理解度確認テスト）
● 試験：第13回までの講義内課題を中心に勉強しておいてください．
● コメント：いつものクイズの要領で，
Goole Form を使った試験を行いました．
40分間で10問という形式でしたが，そこそこ難しい問題もあったのに，
満点の人が3割ぐらいいて驚きました．
受講者のみなさん，お疲れ様でした！