Tomoki Kawahira
/ Graduate School of Economics / Hitotsubashi University
Tomoki Kawahira
/ Graduate School of Economics / Hitotsubashi University
多変数の微分積分学の基礎を学びます．
※ 配布した講義プリント等は manaba の授業ページ（受講者専用）でのみ公開しております．
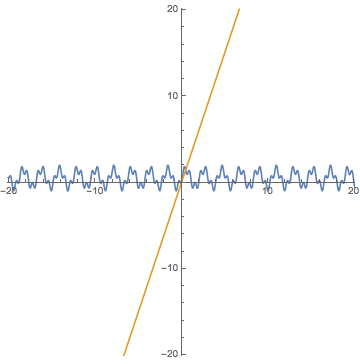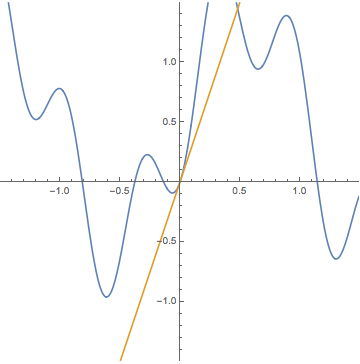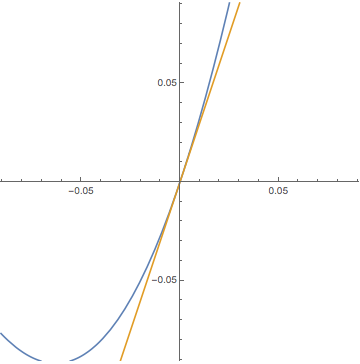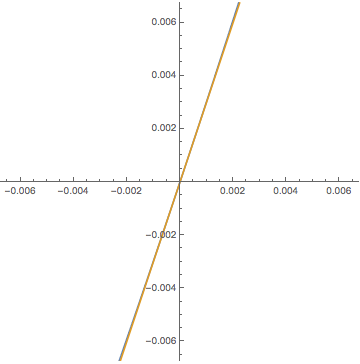
See more GIF animations
第14回 (2020/12/22) 期末試験（オンライン）
いろいろトラブルもありましたがなんとか終わりました．
みなさんお疲れ様です．
第13回(2020/12/15) 体積と曲面積
アンケート自由記載欄への回答と前回の復習．
体積と曲面積の計算例（球と球面など）をやりました．
第12回(2020/12/7) 変数変換（つづき），オンデマンド
アンケート自由記載欄への回答と前回のヤコビアンと
変数変換の累次積分の復習．重積分の変数変換が成り立つ説明と
具体例をやったあと，ガウス積分を計算しました．
第11回(2020/12/1) 変数変換
アンケート自由記載欄への回答と前回の累次積分の復習．
累次積分について追加で演習をしたあと，
変数変換の「ヤコビアン」とその幾何学的意義（これが難しかったようです），
重積分の変数変換の公式についてやりました．
次回はその公式の導出方法と具体例をやりたいと思います．
第10回(2020/11/24) 累次積分
アンケート自由記載欄への回答をしたあと，前回やった
区画上の重積分の定義を復習．
一般領域上の重積分や面積確定集合の定義を与えました．
次にタテ線集合，ヨコ線集合を導入し，
その上での連続関数の累次積分その重積分と一致することを説明しました．
第9回(2020/11/17) 重積分
アンケート自由記載欄への回答をしたあと，前回の復習．
そのあと，重積分の定義について説明しました．
一方的に定義を述べた感じになってしまいましたが，
具体的な計算方法については次回やります．
第8回(2020/11/10) 極大と極小
アンケート自由記載欄への回答をしたあと，前回の復習．
2次の1変数テイラー展開を用いた極大・極小の判定法を紹介したあと，
2次の2変数テイラー展開の再解説，証明のスケッチ，具体例をやりました．
また，これを用いた極大・極小・鞍点の判定法を紹介しました．
次回は判定法の具体的な活用方法について考えます．
第7回(2020/10/27) テイラー展開
アンケート自由記載欄への回答をしたあと，前回の復習．
高階偏導関数，C^n級関数を定義し，
2次のテイラー展開に関する定理の主張と具体例をやりました．
次回はその応用を考えます．
第6回(2020/10/20) 合成関数の微分2（変数変換）
アンケート自由記載欄への回答をしたあと，前回の復習．
変数変換による合成関数の微分が，
やはり勾配ベクトルと速度ベクトルによって
与えられることを説明しました．
第5回(2020/10/13) 合成関数の微分
アンケート自由記載欄への回答をしたあと，前回の復習．
等圧線と風の分布が観れるアプリも紹介しました．
次に1変数の合成関数の微分を思い出しつつ，
1変数->2変数->1変数型の合成関数の微分公式を解説．
具体例をやったところで終わりました．
第4回(2020/10/6) 偏微分とC1級関数
最初にアンケートの回答を紹介，
前回の復習．全微分に現れる定数の
幾何学的な意味を説明し，
偏微分係数を定義．C^1級関数が全微分可能性の十分
条件となることを解説しました．
第3回(2020/9/29) 1次近似と全微分可能性
最初にアンケートの回答を紹介，
ついで前回の復習（とくに「極限」と「連続性」について）．
次に，1変数関数の「微分可能性」について復習．
定義を接線の方程式が見える形にアップデート．
そのノリで2変数関数の「全微分可能性」を定義しました．
ランダウの記号を使わない新しいアプローチですが，
受講者のみなさんの反応はいかがかな．．
第2回(2020/9/22) 多変数関数の極限と連続性
最初にアンケートの回答を紹介．前回の復習，とくに内積の部分を確認したあと，
2変数関数の極限と連続性について，例題を交えながら説明しました．
第1回(2020/9/15) 多変数関数のグラフ，ベクトルの内積
多変数関数の３次元グラフ，等高線グラフについて具体例をみたあと，
1変数関数の等高線がどのような形になるか，
ベクトルの内積を用いて調べました．