 fig 1
fig 1
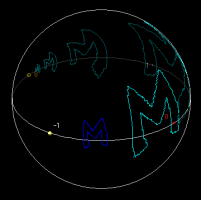 fig 2
fig 2
実数 a, b, c, dに対し,関数 T(z)=(az+b)/(cz+d) はリーマン球面から自身への関数を定め…実係数メビウス変換と呼ばれます. Javaアプレット・Moebius は実係数メビウス変換(および複素アファイン変換)の作用を,実際に球面上に視覚化するためのプログラムです.高校・大学初年級向けのプレゼンテーションに適しています.(参考)
T(z)=(az+b)/(cz+d) の4つの詣数 a, b, c, d は…ヂプレット下段にあるテネベトボッハベで編舜できます‥
注意! 新しい係数を入力したら,Clear/Resetボタンを押して変更を反映させてください.
Normalizeボタンを押すと,係数 a, b, c, d が a/K, b/K, c/K, d/K (ただし,K は |ad - bc| の平方根)に置き換えられます.この操作で T の関数としての作用は変わりませんが, ad - bc = +1 または ad - bc = -1 となり…何かと都合がよいのです‥ちなみに ad - bc = 0 となる場合(このとき t は定数関数)… zero determinant と警告されます‥
また,Complex Affineをチェックすると,実係数メビウス変換のかわりに複素係数アファイン変換 T(z)=(a + bi)z + c + di による作用が表示されます‥この場合…上述のNormalizeボタンは機能しません.
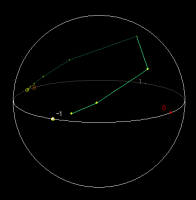
アプレットがスタートすると,リーマン球面と実軸に対応する円が表示されます.(ただし,無限遠点は8で表示.) マウスカーソルがこの上を動くとき,アプレットはカーソルがリーマン球面の画面前方に近い側半分の上を動いていると認識します.一番下に表示されている Re z, Im z が対応する点の座標です.また,リーマン球面は複素平面の上に置かれており,そこからの射影をもとに座標は計算されます.したがって,リーマン球面内側の向き付けが複素平面の向き付けに対応します.小さな黄色い円は T(z) の固定点を表します.
この球の上をマウスでドラッグすると,対応する点の T による軌道が表示されます.軌道の各点は黄色い点で表示され,それぞれ緑色の線で結ばれます(fig 1).
視点を変えたい場合,まずRotate Sphereボタンを押し,球の上をマウスでドラッグすれば球を回転させることができます.
また,Real Axisのチェックをはずすことで,実軸の表示・非表示を切り替えることができます..
 fig 1
fig 1
 fig 2
fig 2
球面上に自由に描いた曲線に対し,その T による像と T の逆変換による像を表示させることができます.
まず,Set Marksボタンを押してください.つぎにマウスをドラッグし,好きな曲線を一筆描きします.曲線といっても,アプレットが処理しているのはいくつかの点を細かい線分で結んだものです. これらの点の個数はSet Marksボタンに表示されます.
ここでForward Imageボタンを押すと,この曲線の T による像が水色で表示されます.さらに T を作用させたいときは,もう一度このボタンを押します.(fig 2)
同様に,Backward Imageボタンを押すと,この曲線の T の逆変換による像が緑色で表示されます.(fig 2)
曲線を消して元の状態に戻すには,Clear/Resetを押してください.
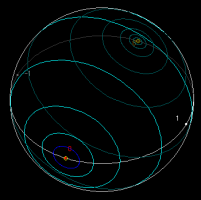 fig 3
fig 3
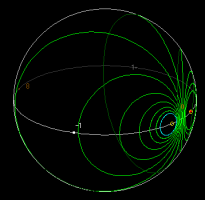 fig 4
fig 4
メビウス変換には「リーマン球面上の円をリーマン球面上の円に写す」という性質があります.曲線をマークする代わりに円をマークするには: (1) Set Circleをチェックする. (2) Set Marksを押す. (3) マウスのボタンをリーマン球面の上で押し,描きたい円の(複素平面上での)中心を選ぶ. (4) マウスをドラッグして描きたい円を選ぶ .(内部計算上の理由により,無限遠点近くを通る円はうまく選択できません.)あとは上と同様に,Forward Image,Backward Imageボタンを使ってその T による作用を見ることができます(fig 3, 4).
各点の軌道を結ぶ緑色の線分は,Segmentのチェックを外すと表示されなくなります.また,マークした曲線(円)と前方・後方軌道の曲線(円)はそれぞれいくつかの点を細かい線分で結んだものですが,これらの線分の表示も同時に解除され,かわりに点自体が太く表示されます.
Circle Danceをチェックすると,ドラッグ時に表示される各点の軌道にそって円が表示されます.これはマウスカーソルの周りに描かれた青い円が軌道上でどのように拡大・縮小されていくかを大まかに表示するものです.これらの円の半径は T の微分係数をもとに計算されていますが,あくまで装飾と考えたほうが良いでしょう.