Tomoki Kawahira
/ Graduate School of Economics / Hitotsubashi University
Tomoki Kawahira
/ Graduate School of Economics / Hitotsubashi University
1変数および多変数の関数について，微分積分学の基礎を学びます．
講義で配布したプリントをまとめたもの：
PDF
See more GIF animations
第1回(2020/12/4) 数列の収束と上限・下限
誤差の話から数列の収束性のε-N 式の定義を説明．
簡単にその性質を確認しました．
上限と下限については次回詳しくお話しします．
第2回(2020/12/7) 実数の連続性，単調列，区間縮小法（オンデマンド）
数列の極限の値を知らない状態で，いかにして極限の存在を保証するか？
という問題をテーマに，実数の連続性の公理（上限・下限の存在），
有界単調列の収束，区間縮小法の原理について解説しました．
コーシー列については次回やります．
第3回(2020/12/11) コーシー列，関数の極限，連続性，最大値（オンデマンド）
前回やり残したコーシー列について，ゆっくりめに詳しく解説．
そのあと，ε-δ式の関数の極限の定義，
連続性の定義，および閉区間における最大値の存在について解説しました．
講義プリントには中間値の定理についても書きましたが，
そちらはまた次回に．
第4回(2020/12/14) 中間値の定理，ロルの定理，平均値の定理
中間値の定理を方程式の数値解法という視点で解説．
ロルの定理，平均値の定理に証明を与えて，
平均値の定理の応用（微分が 0 なら定数関数，など）をやりました．
ロピタルの定理は次回に．
第5回(2020/12/18) テイラー展開
前回の復習のあと，ロピタルの定理（を使うことの難しさ）を説明．
高階導関数やC^n級関数の概念を定義し，
テイラー展開の意義と主張を述べました．
証明や応用については詳しくは次回にやります．
第6回(2020/12/21) テイラー展開の応用
テイラー展開の証明を解説したあと，
テイラー展開の例として指数関数のマクローリン展開，
e の近似計算，三角・対数関数のマクローリン展開を紹介．
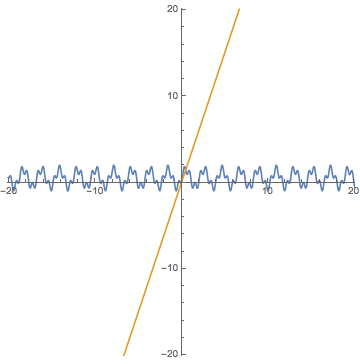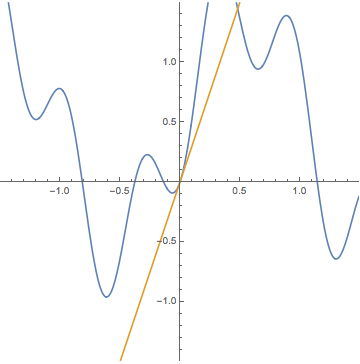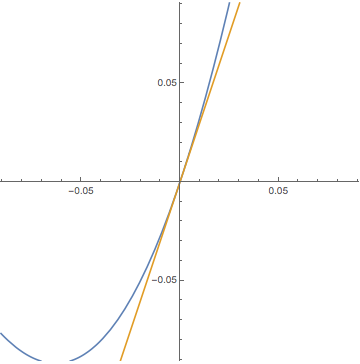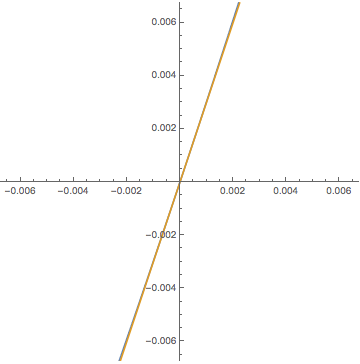
Mathematica によるテイラー多項式のグラフも
デモンストレーションしました．
テイラー級数の話は次回に．
第7回(2020/12/25) 一様連続性と定積分
前回のテイラー展開のごく簡単な復習．
一様連続性の定義と具体例，十分条件（閉区間上の連続関数は一様連続）
について解説，さらに
積分可能性の厳密な定義とその十分条件（閉区間上の連続関数は積分可能）
について解説．
最後に，リーマン和と定積分の誤差に関する定理を述べておわりました．
詳しくは次回やります．
また，前回テイラー展開の証明を解説するのを忘れていたので，
それは年明けの次回ということにさせてください．
第8回(2021/1/8) 点集合・多変数関数の極限と連続性
前回，いや前々回にやり忘れていたテイラー展開の証明を紹介（n=2の場合）．
前回の一様連続性と定積分について復習したあと，
そのあと，n次元ユークリッド空間の基本性質と
開集合・閉集合・領域の定義などをやりました．
極限や連続性についてはやる時間がなかったので，
次回ちゃんとやります．
第9回(2020/1/14) 多変数関数の微分
点列の極限の関数の極限，連続性をやったあと，
前回のアンケートに対する回答で休憩．
1次関数の話と全微分の定義をしたところで終わりました．
第10回(2021/1/18) 合成関数の微分
前回の復習を一通りやったあと，前回のアンケートに対する回答．
偏微分を一般次元でやったあと，合成関数の微分について，勾配ベクトルを用いて説明．
具体例は次回やります．
第11回(2021/1/22) テイラー展開と極大・極小
前回の復習のあと，合成関数の微分公式の具体例をやりました．
そのあと，1変数関数の極大・極小の判定に2次のテイラー展開を用いる方法を解説し，
2変数関数の2次テイラー展開とその証明のスケッチをやりました．
第12回(2021/1/25) 級数の収束・絶対収束
前回の復習のあと，2変数関数の2次テイラー展開の具体例と，
極大・極小・鞍点の判定法についてやりました．
第13回(2021/1/29) べき級数
極大・極小・鞍点の判定法の具体例をやったあと，
複素数列が定める級数の収束・発散・絶対収束
についてその定義と意味を学びました．
べき級数の残りの部分に関してはプリントに加え，
ビデオを提供します．
詳しくはOCW-iの講義ページをご覧ください．