Back to Courses | Home

微分積分　I （2021年度春夏学期 / 火曜3限 / 川平担当）

1変数の微分積分学を学びます．
配布した講義プリントをまとめたものはこちら： PDF
※　配布した講義プリント等は manaba の授業ページ（受講者専用）でのみ公開しております．

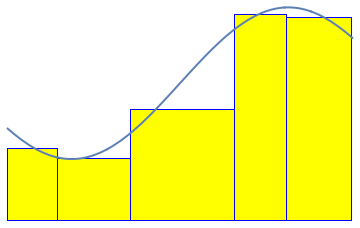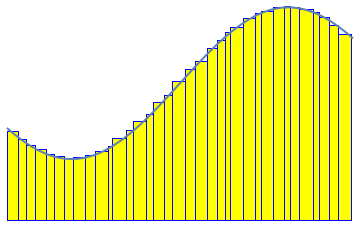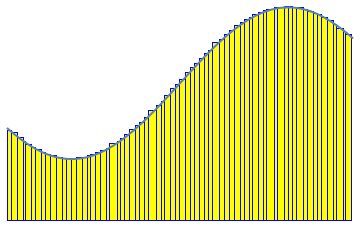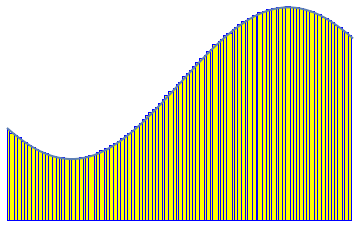
See more GIF animations

第14回(2019/07/19)　期末試験
●　オンラインにて実施し，無事に終了しました．

第13回(2021/07/12)　置換積分と部分積分
●　置換積分（とその具体例），部分積分（とその具体例）について 解説しました．

第12回(2021/07/5)　定積分と微分積分学の基本定理
●　定積分の定義のあと，微分積分学の基本定理と，その応用としての積分計算をやりました．

第11回(2021/06/28)　テイラー展開の応用
●　テイラー展開の具体例として指数関数の場合を計算し， 応用として e の数値計算をやりました．ごく簡単に，平均値の定理の応用と凹凸の判定の話をしました． 定積分の定義までやりたかったのですが，次回にまわしたいと思います．

第10回(2021/06/21)　テイラー展開
●　高階導関数を定義し，テイラー展開の主張を述べました （証明はプリントにもありますが，次回プロジェクターで簡単に説明します．）． 具体例と応用例があまりやれなかったので，それは次回に．

第9回(2021/06/14)　対数微分法，ロルの定理
●　合成関数の微分公式の例題をやった後，逆関数の微分，対数微分法について解説． テイラー展開への準備としてロルの定理の説明をしました．

第8回(2021/06/7)　微分と1次近似
●　微分可能性の定義から関数の1次近似式（接線の方程式）を求め， 数値計算に応用しました．また，ライプニッツ則などの1次近似式による説明をしました．

第7回(2019/05/31)　逆三角関数・微分可能性
●　三角関数の復習．その定義域をうまく制限することで，逆三角関数を定義しました． そのあと，微分可能性の定義と接線の関係を確認しました．

第6回(2019/05/24)　逆関数と指数・対数関数
●　真に単調増加（減少）な関数に対し逆関数が定義できることを確認し， （eを底とする）指数関数の逆関数として対数関数を定義しました．

第5回(2019/05/17)　中間値の定理
●　中間値の定理の主張と証明をやりました．方程式の数値解法である二分法をベースにした構成的な証明です．連続関数の最大・最小値の存在について解説しました．

第4回(2019/05/10)　関数の連続性
●　関数の極限の四則（和差積商）と「はさみ打ちの原理」に関する補足のあと， 極限の練習問題をやってもらいました． さらに「連続関数」を定義．連続関数が和差積商によって 豊富に生成されることを説明しました．

第3回(2019/04/26)　関数の極限
●　e の存在について復習．そのあと，関数や変数とは何か定義を確認しました． また，関数の極限を数列の場合と同様に定義しました．

第2回(2021/04/19)　実数の連続性とe
●　極限の存在を保証する「公理」として，「実数の連続性」について説明しました． 最後にちょこっとだけ，eの定義を述べました．

第1回(2021/04/12)　数と極限
●　実数の存在に関するお話と「数列が収束する」という言葉の定義をし，幾つかの具体例をやりました．

Back to Courses | Home