Back to Courses | Home

古典解析 （2021年度夏学期 / 月曜1限・木曜1限 / 川平担当）

複素関数論を学びます．
講義資料（複素関数の基礎のキソ）： PDF
参考書（入門　複素関数）： サポートページ
※　その他，配布した講義プリント等は manaba の授業ページ（受講者専用）でのみ公開しております．

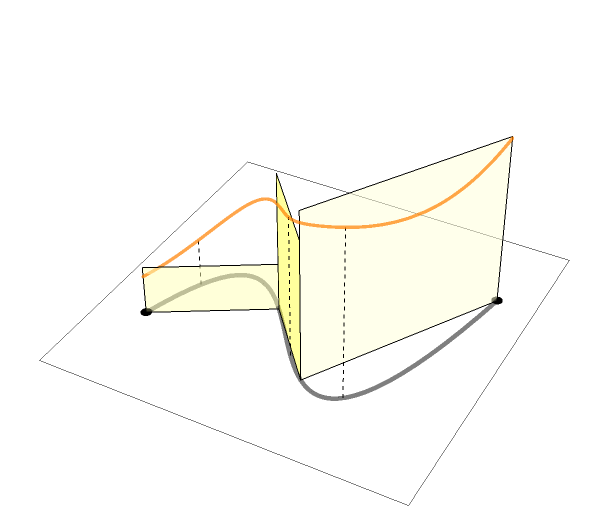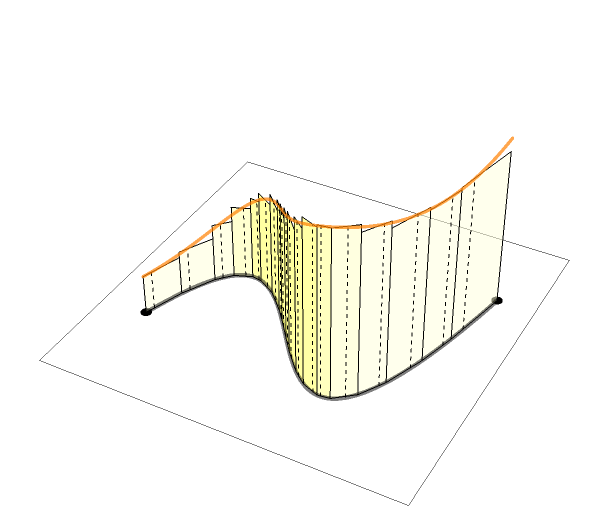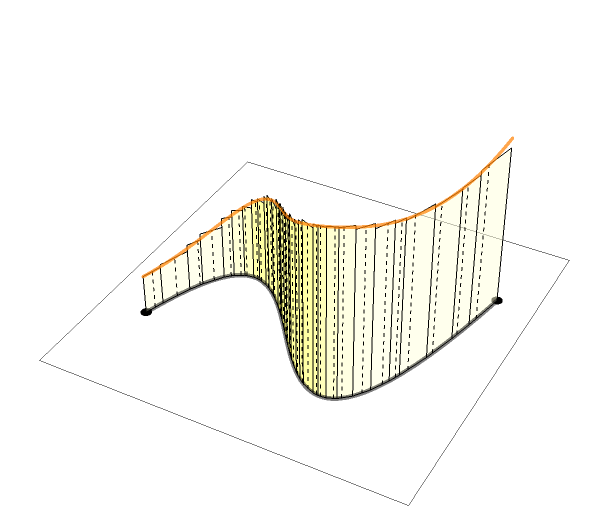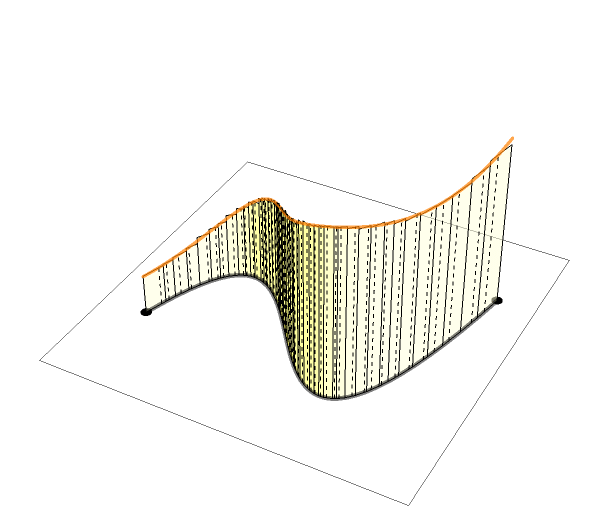
See more GIF animations

第14回(2021/07/19)　期末テスト
●　毎回のクイズと同様の形式で，オンラインで行いました．

第13回(2021/07/15)　留数定理と実積分への応用
●　プロジェクタ上で前回の復習．留数定理の主張をのべて，留数の計算に使える公式とその応用，とくに実積分への応用について解説しました．最後は時間がなかったので，再びプロジェクタ上で説明しました．

第12回(2021/07/12)　ローラン展開と留数
●　プロジェクタ上で前回の復習とコーシーの積分公式の証明，リュービルの定理の証明をやりました．級数の収束性を定義したあと，穴あき円板上のローラン展開を述べ，穴を埋めた特別な場合としてテイラー展開が得られることを示しました．さらに，積分とローラン展開の(-1)次の係数の関係を説明し，留数の定義をしました．

第11回(2021/07/08)　積分公式
●　プロジェクタ上で前回の復習．前回からの続きで，実積分への応用の話をやりました．さらに，コーシーの積分公式，高階微分の積分公式を述べたあと，応用としてリュービルの定理，代数学の基本定理，最大値原理（弱い形）について説明しました．

第10回(2021/07/05)　積分定理の応用
●　プロジェクタ上で前回の復習と積分定理の証明の概略（グリーンの定理を用いる）をやりました．応用として積分路の変形，基本公式その2（講義資料参照）をやりました．さらに基本公式の応用として，複素積分の計算や実積分の応用（次回へ続く）についてやりました．

第9回(2021/07/01)　コーシーの積分定理
●　プロジェクタ上で前回の復習．複素線積分を計算するためにパラメーターによる「置換積分」を説明し，具体例として「基本公式その１」（講義資料参照）をやりました． コーシーの積分定理の主張について説明しました．

第8回(2021/06/28)　複素線積分
●　プロジェクタ上で前回の復習．積分路となる「区分的に滑らかな曲線」を定義し，「実関数の定積分」にそう形で複素線積分を定義しました． このままでは計算ができないので，計算できるようにパラメーター表示（「置換積分」）する方法を次回学びます．

第7回(2021/06/24)　コーシー・リーマンの方程式の応用
●　プロジェクタ上で前回の復習と，コーシー・リーマンの方程式の導出（照明の概略）をやりました．また，Mathematicaを用いて正則な複素関数と正則でない複素関数の違い（小さい正方形をほぼ正方形に写すか，あるいはほぼ平行四辺形に写すか）を確認しました．さらに，コーシー・リーマンの応用として指数関数の導関数が指数関数になることを確認しました． 最後に，実関数の定積分について簡単に復習し，複素線積分のアイディア（イメージ，上のgifアニメーション参照）について説明しました．

第6回(2021/06/21)　正則関数とコーシー・リーマンの方程式
●　プロジェクタ上で前回の復習．正則性を規定するコーシー・リーマンの方程式を導入しました．

第5回(2021/06/17)　複素関数の連続性と微分可能性
●　プロジェクタ上で前回の復習と，前回やらなかった 方程式 sin z = 0 の解について説明． 極限を用いて複素関数の連続性を定式化し， 次に微分可能性を定義，その（幾何学的な）意味を説明しました．

第4回(2021/06/14)　複素三角関数，関数の極限
●　プロジェクタ上で簡単に複素対数関数や複素べきについて解説しました．そのあと，複素三角関数の定義と諸性質について解説しました．複素関数の極限とその具体例を見たところで終了． 連続性まで説明したかったのですが，次回に回します．

第3回(2021/06/10)　指数関数の性質，1のべき根
●　指数関数の指数法則，周期性について証明したあと，指数関数による正方形の像について考えました．また，1のべき根が単位円の等分点として現れることを極形式から導きました．

第2回(2021/06/07)　オイラーの公式と指数関数
●　有名なオイラーの公式を指数関数のテイラー展開から導きますが，この講義では「オイラーの公式が成り立つように」複素指数関数を定義する，という立場をとります．

第1回(2021/06/03)　複素数と複素数平面，極形式
●　複素数の具体的な構成（平面ベクトルを改名）のあと，極形式， 複素数の積に関する幾何学的性質（積の偏角は偏角の和）を確認しました．

Back to Courses | Home