Tomoki Kawahira
/ Graduate School of Economics / Hitotsubashi University
Tomoki Kawahira
/ Graduate School of Economics / Hitotsubashi University
曲線と曲面の幾何学を学びます．
この講義について：
PDF
幾何学 I の講義プリント：
PDF
※ その他，配布した講義プリント等は manaba の授業ページ（受講者専用）でのみ公開しております．
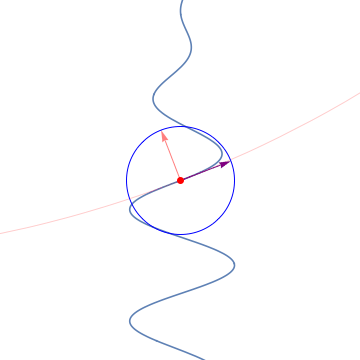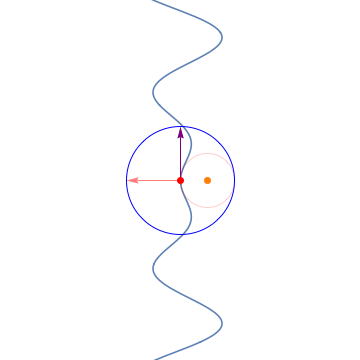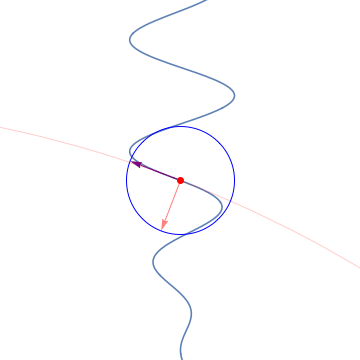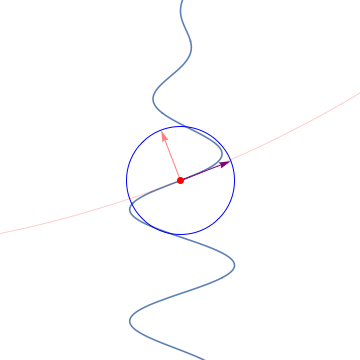
See more GIF animations
第28回(2021/12/21) 期末試験
● オンラインで期末試験をやりました．
第27回(2021/12/17) ガウス・ボンネの定理 (2) ，オンデマンド
● 「頂点」あるいは「角」をもった「三角形」を定義し，それに対するガウス・ボンネの定理について解説（証明）．具体例として測地三角形のガウス・ボンネを紹介しました．つぎにオイラー数を定義と具体例を説明して，最後に閉曲面に対するガウス・ボンネの定理を証明しました．
第26回(2021/12/14) ガウス・ボンネの定理 (1) ，オンデマンド
● 1-形式および2-形式に対し，それぞれの積分を定義．グリーンの定理を証明なしで紹介したあと，滑らかな閉曲線で囲まれた「穴のない」曲面に対しガウス・ボンネの定理を証明しました．
第25回(2021/12/10) 測地線
● 曲面上の曲線に対し，測地的曲率と法曲率を定義し，測地線を「測地的曲率0の曲線」として定義しました．また，次回のガウス・ボンネの定理に向けて，測地的曲率が満たすべき方程式を導きました．
第24回(2021/12/3) 等長地図はなぜできない？
● ガウス驚異の定理の証明とその意義を解説．構造方程式から第一基本形式が定まる具体例やりました．最後に等長地図はなぜできないのか，という事実をガウス曲率を用いて解説しました．
第23回(2021/12/3) ガウス驚異の定理
● フルネ・セレの公式の曲面版から曲面の第1構造式および第2構造式（カルタンの構造式）を導き，ガウス驚異の定理の主張をのべました．
驚きポイントがわかりづらいのでそれについては証明とともに次回お話しします．
第22回(2021/11/30) 微分形式と第2基本形式
● フルネ・セレの公式の曲面版を導いたあと，接ベクトル空間の正規直交基底を用いて第2基本形式を書き直しました．
第21回(2021/11/26) 微分形式と第1基本形式
● 接ベクトル空間の正規直交基底を用いて第1基本形式を書き直しました．
第20回(2021/11/23) 微分形式
● 「驚異の定理」に至る準備として，微分形式と外微分（の非常に簡単なバージョン）を定義しました．
第19回(2021/11/16) 具体例つづき，極小曲面とプラトー問題
● さらなる具体例としてトーラスをやりました．
平均曲率の意義を説明するために，プラトー問題の解が
平均曲率 0 の曲面（極小曲面）となることを示しました．
第18回(2021/11/12) 具体例
● 具体例として円柱，球面について
ワインガルテン行列，ガウス曲率，平均曲率を計算しました．
第17回(2021/11/9) ガウス曲率と平均曲率
● 法平面を法線ベクトルを軸に回転させて，
断面として現れる曲線の曲率の最大値と最小値を求めます．
（ラグランジュの未定乗数法の勉強・復習も兼ねる．）
ワインガルテン行列，ガウス曲率，平均曲率を定義しました．
第16回(2021/11/6) 第2基本形式と曲面の形
● 曲面上のある点から単位法線ベクトルを「立て」，その方向に関する高さ関数を考えることで，第2基本形式はヘッセ行列とみなせます．このことから，曲面の形状（凹凸，鞍点）に関する情報を得る方法について説明しました．
第15回(2021/11/2) 幾何学II 初回： 第2基本形式
● 曲面の法平面による切り口として現れる曲線に対し曲率を考えて，
それを元に第２基本形式を定義しました．
第14回(2021/10/29) 幾何学I 期末試験
● オンラインのGoogle Formsで期末試験をやりました．
第13回(2021/10/26) 第1基本形式 (2)
● 第1基本形式を用いて，地図から読み取った情報から
実物の曲線や交差角，面積を測る方法を解説しました．
第12回(2021/10/22) 第1基本形式
● 曲面（地球）上の曲線の長さや交差角を地図から読み取るには？
という問いに答える形で，第1基本形式を導出しました．
第11回(2021/10/19) 滑らかな曲面の地図づくり
● 具体例といて球面を考えながら，パラメーター集合を与える
領域を地図とみなす考え方について紹介しました．
第10回(2021/10/15) 接平面と曲面積
● 1次近似をもちいて接平面の式を導出しました．
また，曲面積の公式（定義式）を与えました．
第9回(2021/10/12) 滑らかな曲面
● 滑らかな曲線の考え方をもとに，滑らかな曲面を定義しました．
第8回(2021/10/8) 空間曲線の基本定理
● 捩率が 0 であれば平面に含まれることを証明しました．
弧長パラメーターを用いない曲率と捩率の公式，
ブーケの公式，空間曲線の基本定理について概説しました．
第7回(2021/10/5) κとτ
● 曲率と捩率の幾何学的な意味を解説し，具体例として常らせんに対して曲率と捩率を計算しました．
第6回(2021/10/1) 空間曲線
● 空間曲線の定義，曲率，捩率の定義をやりました．
第5回(2021/09/28) 平面曲線の基本定理
● 実用上重要なクロソイド曲線の話や，平面曲線の基本定理について解説しました．
第4回(2021/09/24) 収束円
● プロジェクターを用いて前回の復習を25分ほど．短くできないのはなぜ？
曲率の幾何学的な意味を説明したあと，フルネの公式，曲率円について解説．
一般パラメーター表示に対する曲率の公式を紹介したところでタイムアウト．
2分ぐらい延長してしまった気がします．
第3回(2021/09/21) 孤長パラメーターと曲率
● プロジェクターを用いて前回の復習を20分ほど．弧長パラメーターとその具体例（円とか）をしたあと，曲率の定義をしたところであえなく終了．
第2回(2021/09/17) 曲線と速度
● プロジェクターを用いて前回の復習を20分ほど．
平面曲線の定義，速度ベクトル，長さを具体例とともにやりました．
第1回(2021/09/14) ベクトルの内積と外積
● 講義の概要を述べたあと，一般次元のユークリッド空間とその内積，3次元の場合の外積の定義と性質を復習しました．途中，休憩を入れるのを忘れていました．